개발자가 N진수를 알아야하는 이유
사람에겐 3과 5를 더하는 것이 익숙하기 때문에 주어진 수를 이용하여 바로 계산이 가능하지만,
컴퓨터는 그렇지 않다.
컴퓨터는 사람이 계산하는 방식과 다른 원리로 계산을 한다.
이 원리를 이해하기 위해서는 '진수' 라는 개념에 대한 이해가 필요하다.
진수란?
진법으로 나타내어진 수를 의미한다
n진법이란? 0부터 n개의 숫자를 사용해서 수를 표현하는 방법이다. 즉,0~ (n-1) 까지 표현한다.
n진법으로 나타낸 수가 n진수이다.
이것을 알면 각 진법을 간단히 생각할 수 있다.
2진법이란, 0~1까지의 2개의 숫자를 사용해서 수를 표현한다.
8진법이란, 0~7 까지의 8개의 숫자를 사용해서 수를 표현한다.
16진법이란, 0~9 까지의 10개의 숫자를 사용하고 남는 자리는 A~F 까지 6개의 문자를 사용해서 수를 표현한다.
지금부터 각각의 진법에 대해 조금 더 자세히 알아보자.
10진수
표현할 수 있는 숫자가 0,1,2,3,4,5,6,7,8,9 로 10개라서 10진수이다.
0~9 까지의 10개의 숫자를 세다가 더이상 표현 수가 없을때 높은 자릿수를 1씩 증가시켜 다음의 수를 표현한다.
아래의 예시를 보자.

위와 같은 방식이 우리가 일상 생활에서 사용하고 있는 10진수이다.
2진수
표현할 수 있는 숫자가 0, 1 로 2개라서 2진수이다.
0~1 까지 2개의 숫자를 세다가 더이상 표현 수가 없을때 높은 자릿수를 1씩 증가시켜 다음수를 표현한다.
아래의 예시를 보자.

위와 같은 방법이 2진수이다.
10진수가 0,1,2,3,4,5 ... 로 표현될 때
2진수는 0,1,10,11,100,101 ... 로 표현되는 것이다.
8진수
표현할 수 있는 숫자가 0,1,2,3,4,5,6,7 로 8개라서 8진수이다.
아래의 예시를 보자.

위와 같은 방법이 8진수 이다.
10진수가 0,1,2,3,4,5,6,7,8,9,10 ... 로 표현될 때
8진수는 0,1,2,3,4,5,6,7,10,11,12 ... 로 표현된다.
8진수에서는 10은 10진수에서 8이라는 값에 해당한다,
8진수에서 11은 10진수에서 9라는 값에 해당한다.
8진수에서 12는 10진수에서 10이라는 값에 해당한다.
16진수
표현할 수 있는 숫자 0,1,2,3,4,5,6,7,8,9 에 문자 A,B,C,D,E,F 까지 16개라서 16진수이다.
아래의 예시를 보자.
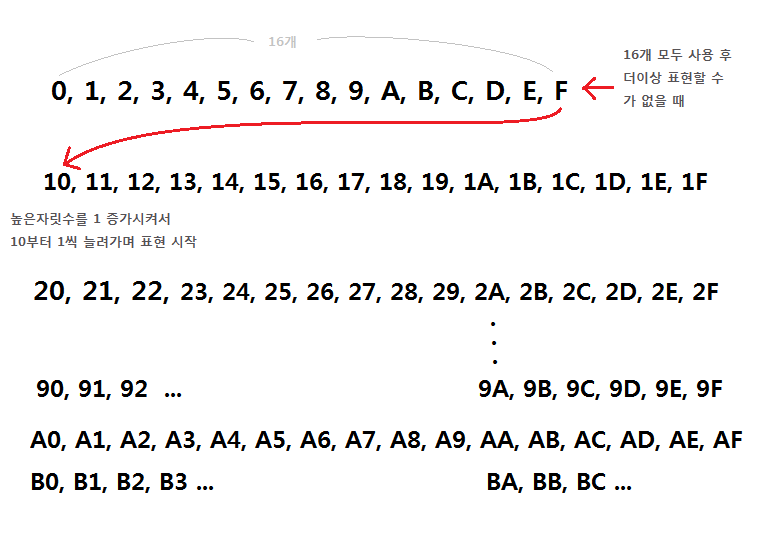
위와 같은 방법이 16진수이다.
10진수가 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 ... 로 표현될때
16진수는 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F ... 로 표현된다.
A는 십진수로 10
B는 11
C는 12
D는 13
E는 14
F는 15 의 값에 해당한다는 사실을 알아두면, 16진수를 10진수로 변환할때 좀 더 수월하다.
지금까지 2진수,8진수,16진수의 개념과 원리에 대해 알아보았다.
지금부터는 각각의 변환법에 대해 알아보자.
2진수, 8진수, 16진수 -> 10진수로 변환
각 진수변환법에대해 복잡한 수까지 완벽하게 계산하는 연습을 할 필요는 없다.
사실 진수변환기와 진수표는 검색을 통해 언제든 쉽게 찾아볼 수 있다.
하지만 어떤 원리로, 어떻게 변환되는지와 간단한 수의 변환법은 알아 둘 필요가 있다.
각 진수별 변환법은 전부 동일하다.
뒤에서부터 n번째 자릿수가 n-1승이된다.
그리고 그 자릿수 별 해당하는 숫자 x 진수의 n-1승을 전부 합한 것이 10진수값이다.
위의 설명을 보고 잘 모르겠다면, 아래의 예시들을 보며 이해할 수 있을것이다.
2진수를 10진수로 변환하는 과정
다음 예시는 2진수의 11010 을 10진수로 변환하는 과정이다.

뒤에서부터 n번째 자릿수가 n-1승이된다
뒤에서 1번째 자리는 2의 0승
뒤에서 2번째 자리는 2의 1승
뒤에서 3번째 자리는 2의 2승
뒤에서 4번째 자리는 2의 3승
뒤에서 5번째 자리는 2의 4승이다.
그 자릿수에 해당하는 숫자와 2의n-1 승을 곱해서 더해준것이 2진수의 십진수 변환이다.
8진수를 10진수로 변환하는 과정
다음 예시는 8진수의 150을 10진수로 변환하는 과정이다.

뒤에서부터 n번째 자릿수가 n-1승이된다.
뒤에서 1번째 자리는 8의 0승
뒤에서 2번째 자리는 8의 1승
뒤에서 3번째 자리는 8의 2승
그 자릿수에 해당하는 숫자와 8의n-1 승을 곱해서 더해준것이 8진수의 십진수 변환이다.
16진수를 10진수로 변환하는 과정
다음 예시는 16진수의 2AD를 10진수로 변환하는 과정이다.

뒤에서부터 n번째 자릿수가 n-1승이된다.
뒤에서 1번째 자리는 16의 0승
뒤에서 2번째 자리는 16의 1승
뒤에서 3번째 자리는 16의 2승
그 자릿수에 해당하는 숫자와 16의n-1 승을 곱해서 더해준것이 16진수의 십진수 변환이다.
10진수 -> 2진수, 8진수, 16진수 로 변환
각 진수별 변환법 역시 동일하다.
변환하고자 하는 10진수를 각 진수로 나눌 수 없을 때 까지 나눈 후 '마지막 남은 몫' 과 '나머지' 를 읽어준다.
10진수로 175 라는 숫자를 각 진수별로 변환해보겠다.
10진수를 2진수로 변환하는 과정
다음은 2진수의 변환예시이다.

10진수를 8진수로 변환하는 과정
다음은 8진수의 변환예시이다.
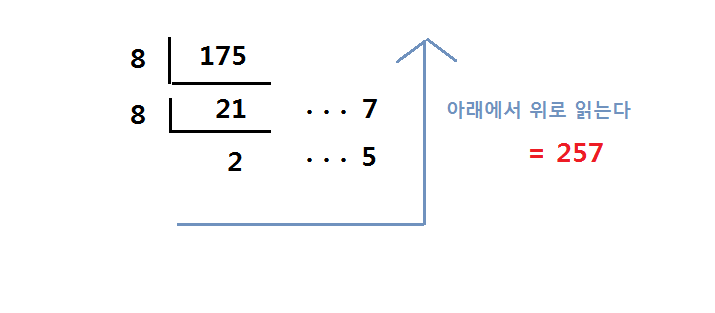
10진수를 16진수로 변환하는 과정
다음은 16진수의 변환예시이다.

2진수와 8진수에서는 몫과 나머지를 그대로 붙여 읽었지만,
16진수에서 10~14 라는 숫자는 없다.
해당 수는 16진수에서 A~F 의 문자로 표현하기때문에 반드시 문자로 변형해주어야 한다.
만약 2진수에서 16진수로 변환하거나,
8진수에서 16진수로 변환하거나,
8진수에서 2진수로 변환하거나 등등 을 원한다면
10진수로 변환하는 과정을 중간에 거쳐가면 될 것이다.
8진수를 2진수로 변환하는 과정
간단히 아래의 예시를 보자.
8진수 35 를 2진수로 변환하는 과정이다.

먼저 8진수를 10진수로 변환한 후, 변환한 10진수를 다시 2진수로 변환한 모습이다.
이런 진수들은 왜 사용할까 ?
컴퓨터는 진수의 표현을 전기적인 신호로 판단한다.
컴퓨터는 2진수를 사용하기 때문에 신호의 단계가 두개이다.
전기 신호가 있으면 1, 없으면 0 으로 판단
만약 10진수의 체계를 사용하려면 컴퓨터는 열개의 신호 단계를 거쳐야한다.
전기 신호의 크기를 10단계로 나누면, 신호를 판단할때 오류가 더 늘것이다.
예를들어,
전기 신호의 크기가 5v(5볼트) 라고 가정하자.
10단계의 신호단계에서는 각 단계별로 0.5v 씩의 차이가 있을것이다.
만약 기계결함으로 인해 4.2v의 신호가 전달된다면 어떻게될까?
4.2v는 8단계와 9단계 사이의 신호이다.
4.2v는 4v에 가깝기 때문에 8단계의 신호가 아님에도 불구하고 8단계로 판단되는 오류가 생길 수 있다.
하지만 2진수는 신호가 있거나(1), 없거나(0) 둘 중 하나이다.
있거나 없는것에 중간은 없다.
이러한 이유로 안전한 2진수 체계를 사용한다.
20진수도 아니고 왠지 애매하게 느껴지는 16진수를 사용하는 이유는
16이 2의 4승 이기 때문에 2진수와 4대 1의 변환이 가능하다는 점에서 용이하기 때문이다.
8진수도 마찬가지이다.
십진수로 0부터 15까지 표현하는데에
2진수는 0,1,10,11,100,110,111,1000 ... 이렇게 긴 나열이 필요한 반면,
16진수는 1,2,3,4,5,6,7,8,9,A,B,C,D,E,F 이렇게 한 자릿수로 표현이 가능하기 때문에 2진수보다 효율이 좋다.
작은 수만 해도 이러할진데, 억 단위로 넘어가는 수라면 더 큰 차이가 날 것이다.
실제로 16진수는 억 단위의 10진수도 단 8자리만으로 표현 가능하다.
즉 메모리의 영역 부담을 줄일 수가 있다.
8진수의 사용목적도 16진수와 비슷하지만, 효율이 절반이기때문에 자주 사용하진 않는다.
2진수, 8진수, 16진수의 데이터 표현 방법
우리가 프로그래밍을 하면서 변수에 어떤 값을 저장할 때 10진수는 일상적 표현을 그대로 대입한다.
예를들어 15를 저장하고 싶다면 int a= 15; 와 같이 15라는 숫자를 그대로 대입하면 된다.
하지만 2진수, 8진수, 16진수는 표현법이 따로 정해져있다.
2진수는 대입하고자 하는 값 앞에 0b를 붙인다. (숫자0과 영문자b)
8진수는 대입하고자 하는 값 앞에 0 을 붙인다. (숫자0)
16진수는 대입하고자 하는 값 앞에 0x 를 붙인다. (숫자0과 영문자x)
아래의 예시를 보자.
변수 a,b,c,d 는 모두 10진수 122 이라는 값을 저장하는 코드이다.
122는
2진수로 1111010
8진수로 172
16진수로 7A 이다.

각각 진수의 데이터 표현 방법에 따라 변수에 저장하면,
위와 같이 모두 122라는 값으로 출력된다는 것을 알 수 있다.
반대로 십진수를 2진수, 8진수, 16진수로 변환하여 출력하는 방법도 있다.
아래의 내용은 메서드와 클래스에 관한 지식이 없다면 다소 이해하기 까다롭다.
읽고도 잘 모르겠다면 추후에 공부하는것을 추천한다.
10진수를 n진수로 바꾸어주는 각각의 메서드를 호출하여 나타낼 수 있다.
2진수 변환 메서드 : Integer.toBinaryString(십진수 값);
8진수 변환 메서드 : Integer.toOctalString(십진수 값);
16진수 변환 메서드 : Integer.toHexString(십진수 값);
원래 메서드는 객체 생성 후 객체로 접근하여 호출하는게 일반적이지만,
진수 변환 메서드는 Integer 클래스에 static 으로 선언되어있기 때문에
Integer 클래스를 통해 바로 호출이 가능하다.
위의 메서드는 String 타입으로 도출된다.
바로 출력하는게 아닌, 변수에 초기화 하고싶다면 String타입으로 지정해야 에러가 나지 않는다.
아래 예시를 통해 확인하자.

10진수 122를 각각 2진수,8진수,16진수로 변환하는 메서드를 호출하여
String 타입의 변수 str1, str2, str3 에 초기화했다.
Console창에 보이는 바와 같이
각각의 진수로 변환되어 출력된 모습이다.
'Java > Standard' 카테고리의 다른 글
| Scanner.nextInt() / nextLine() 오류 : 두가지 해결방법 (0) | 2020.06.19 |
|---|---|
| 반복문 : while 과 do~while (0) | 2020.06.18 |
| 반복문 완전 기초 이해하기 : for문 (0) | 2020.06.18 |
| & 와 && 의 차이점과 활용예시 (5) | 2020.06.16 |
| long,float 의 값 뒤에 L,F 을 붙여야 하는 이유 (0) | 2020.06.11 |
